Enter OTP to View Content
JEE Physics Notes
Motion in Two Dimension: Projectile Motion
1. Introduction to Projectile Motion
The motion of an object is called two-dimensional if two of the three coordinates required to specify the position of the object in space change with respect to time. In such a motion, the object moves in a plane. Examples include a billiard ball moving over a billiard table, an insect crawling over the floor of a room, or the Earth revolving around the Sun.
Two special cases of motion in two dimensions are:
- Projectile motion
- Circular motion
In projectile motion, if the force acting on a particle is oblique with its initial velocity, the motion is termed projectile motion. The classic example provided is a hunter aiming a gun at a monkey on a tree. If the monkey drops at the instant the bullet leaves the barrel, the bullet will hit the monkey because the bullet follows a parabolic path, not a linear one. This parabolic motion is characteristic of projectile motion.
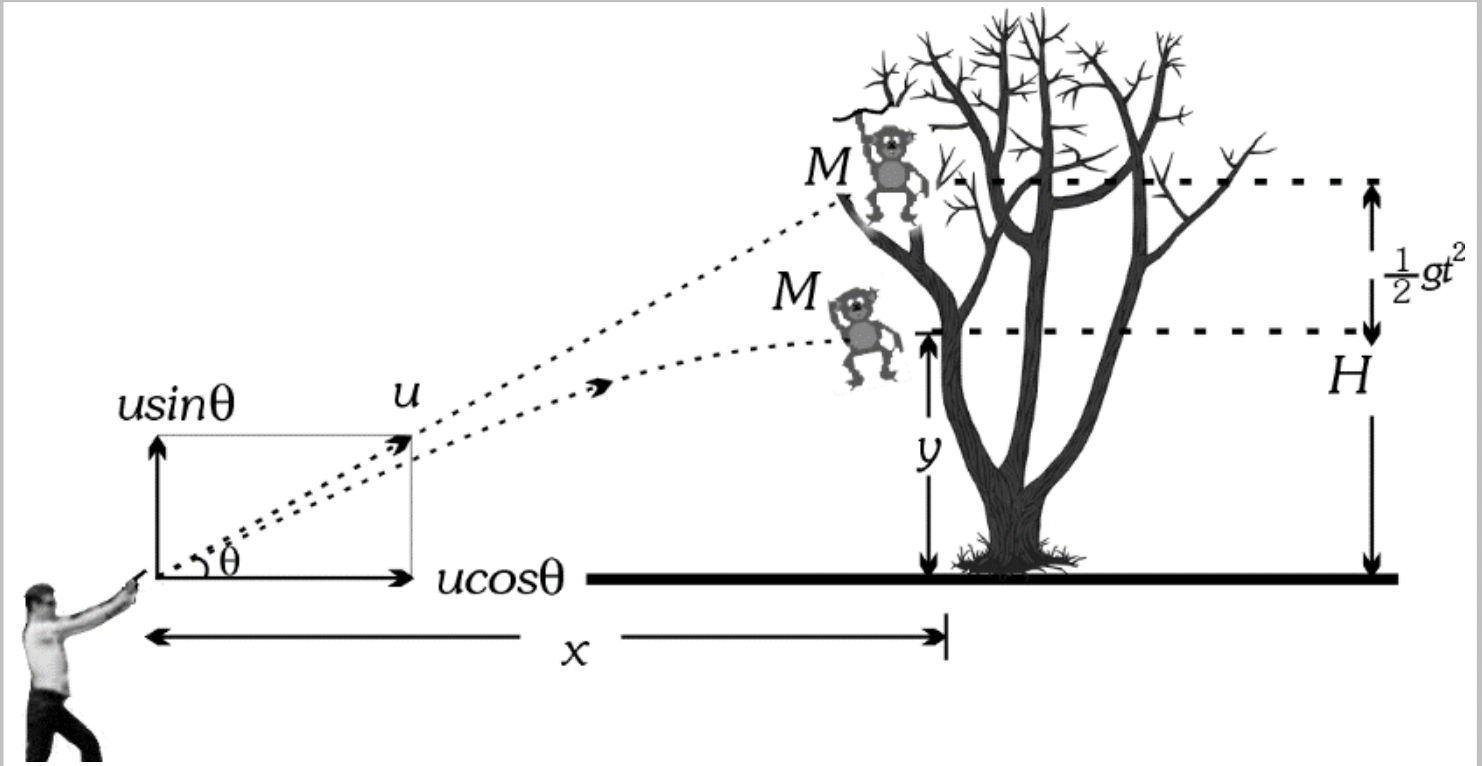
2. What is a Projectile?
A body that is in flight through the atmosphere but is not being propelled by any fuel is called a projectile.
Examples of projectiles:
- A bomb released from an airplane in level flight.
- A bullet fired from a gun.
- An arrow released from a bow.
- A javelin thrown by an athlete.
3. Assumptions of Projectile Motion
For simplifying the study of projectile motion, certain assumptions are made:
- There is no resistance due to air.
- The effect due to the curvature of the Earth is negligible.
- The effect due to the rotation of the Earth is negligible.
- For all points of the trajectory, the acceleration due to gravity ‘$g$’ is constant in magnitude and direction.
4. Principles of Physical Independence of Motions
The motion of a projectile is a two-dimensional motion, which can be analyzed by discussing its horizontal and vertical components independently. This is known as the principle of physical independence of motions.
- The velocity of the particle can be resolved into two mutually perpendicular components: horizontal component and vertical component.
- The horizontal component of velocity remains unchanged throughout the flight (assuming no air resistance).
- The force of gravity continuously affects the vertical component of velocity.
- The horizontal motion is a uniform motion (constant velocity), while the vertical motion is a uniformly accelerated (or retarded) motion due to gravity.
5. Types of Projectile Motion
Projectile motion can generally be categorized into three types:
- Oblique projectile motion (projected at an angle to the horizontal)
- Horizontal projectile motion (projected horizontally from a height)
- Projectile motion on an inclined plane
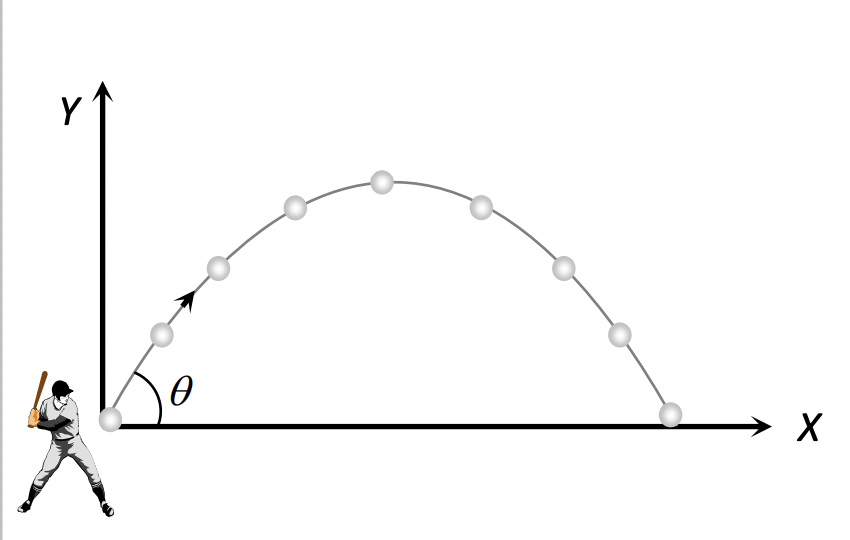
6. Oblique Projectile
In oblique projectile motion, a particle is thrown with an initial velocity ‘$u$’ at an angle ‘$\theta$’ with the horizontal. In this motion:
- Horizontal component of velocity ($u \cos \theta$), acceleration ($g$, downwards), and mechanical energy remain constant.
- Speed, overall velocity, vertical component of velocity ($u \sin \theta$), momentum, kinetic energy, and potential energy all change.
- Velocity and kinetic energy are maximum at the point of projection.
- Velocity and kinetic energy are minimum (but not zero, as horizontal component is constant) at the highest point of the trajectory.
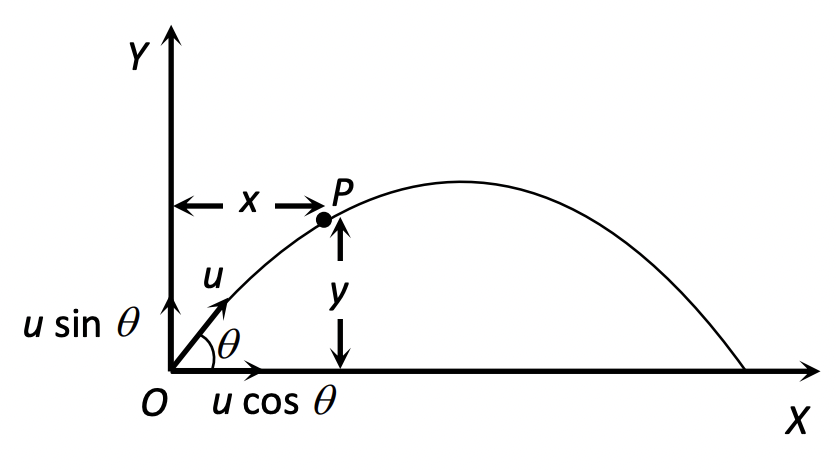
6.1. Vectorial Representation of Projectile Motion
Understanding projectile motion is greatly enhanced by using vector notation for position, velocity, and acceleration. This approach clearly shows the independent nature of horizontal and vertical motions and the constant influence of gravity.
Initial Velocity Vector ($\vec{u}$):
If a projectile is launched with an initial speed $u$ at an angle $\theta$ with the horizontal (positive X-axis), its initial velocity vector can be written as:
$\vec{u} = u_x \hat{i} + u_y \hat{j} = (u \cos \theta) \hat{i} + (u \sin \theta) \hat{j}$
Acceleration Vector ($\vec{a}$):
Under the standard assumptions of projectile motion, the only acceleration acting on the projectile is due to gravity, which is constant and directed vertically downwards. Taking the positive Y-axis upwards:
$\vec{a} = a_x \hat{i} + a_y \hat{j} = 0 \hat{i} – g \hat{j} = -g \hat{j}$
This highlights that the acceleration has no horizontal component ($a_x=0$) and a constant vertical component ($a_y=-g$).
Instantaneous Velocity Vector ($\vec{v}$ at time $t$):
The velocity vector at any time $t$ can be found by integrating the acceleration or by using kinematic equations in vector form ($\vec{v} = \vec{u} + \vec{a}t$):
$\vec{v}(t) = (u \cos \theta) \hat{i} + (u \sin \theta – g t) \hat{j}$
Here, the horizontal velocity component $(u \cos \theta)$ remains constant, while the vertical velocity component $(u \sin \theta – g t)$ changes linearly with time.
Instantaneous Position Vector ($\vec{r}$ at time $t$):
The position vector at any time $t$ can be found by integrating the velocity or by using kinematic equations in vector form ($\vec{r} = \vec{u}t + \frac{1}{2}\vec{a}t^2$, assuming origin as starting point):
$\vec{r}(t) = (u \cos \theta) t \hat{i} + \left((u \sin \theta) t – \frac{1}{2} g t^2\right) \hat{j}$
This vector defines the $(x, y)$ coordinates of the projectile at time $t$.
6.2. Graphical Analysis of Projectile Motion
Visualizing the components of motion through graphs provides a deeper understanding of projectile dynamics:
1. Horizontal Velocity ($v_x$) vs. Time ($t$):
Since $a_x = 0$, the horizontal velocity $v_x = u \cos \theta$ is constant throughout the flight.
$v_x(t) = u \cos \theta$
(Graph would be a horizontal line)
2. Vertical Velocity ($v_y$) vs. Time ($t$):
Since $a_y = -g$ (constant acceleration), the vertical velocity changes linearly with time. It decreases while moving up, becomes zero at the peak, and increases (in negative direction) while moving down.
$v_y(t) = u \sin \theta – g t$
(Graph would be a straight line with negative slope $-g$)
3. Horizontal Position ($x$) vs. Time ($t$):
With constant horizontal velocity, the horizontal displacement increases linearly with time.
$x(t) = (u \cos \theta) t$
(Graph would be a straight line with positive slope $u \cos \theta$)
4. Vertical Position ($y$) vs. Time ($t$):
With constant vertical acceleration, the vertical displacement changes quadratically with time, resulting in a parabolic shape.
$y(t) = (u \sin \theta) t – \frac{1}{2} g t^2$
(Graph would be a parabola opening downwards)
6.3. Equation of Trajectory (Derivation)
Consider a projectile thrown with velocity $u$ at an angle $\theta$ with the horizontal. The velocity $u$ can be resolved into two rectangular components:
- Horizontal component: $u_x = u \cos \theta$ (along X-axis)
- Vertical component: $u_y = u \sin \theta$ (along Y-axis)
For horizontal motion (uniform velocity, $a_x = 0$):
$x = u_x t$
$x = (u \cos \theta) t \quad \Rightarrow \quad t = \frac{x}{u \cos \theta} \quad \cdots (i)$
For vertical motion (uniformly accelerated motion, $a_y = -g$):
$y = u_y t + \frac{1}{2} a_y t^2$
$y = (u \sin \theta) t – \frac{1}{2} g t^2 \quad \cdots (ii)$
Substitute $t$ from equation (i) into equation (ii):
$y = (u \sin \theta) \left(\frac{x}{u \cos \theta}\right) – \frac{1}{2} g \left(\frac{x}{u \cos \theta}\right)^2$
$y = x \frac{\sin \theta}{\cos \theta} – \frac{1}{2} \frac{g x^2}{u^2 \cos^2 \theta}$
$y = x \tan \theta – \frac{1}{2} \frac{g x^2}{u^2 \cos^2 \theta}$
This equation is of the form $y = ax – bx^2$, which is the standard equation of a parabola. Therefore, the trajectory of a projectile is parabolic.
Alternative form of trajectory equation:
$y = x \tan \theta \left[1 – \frac{x}{R}\right]$
Where $R$ is the horizontal range, $R = \frac{u^2 \sin 2\theta}{g}$.
6.4. Displacement of Projectile
Let the particle reach position P with coordinates $(x, y)$ after time $t$ from projection. The position vector $\vec{r}$ of the particle at time $t$ is:
$\vec{r} = x\hat{i} + y\hat{j}$
From the horizontal and vertical motions:
$x = (u \cos \theta) t$
$y = (u \sin \theta) t – \frac{1}{2} g t^2$
Substituting these into the position vector:
$\vec{r} = (u \cos \theta) t \hat{i} + \left((u \sin \theta) t – \frac{1}{2} g t^2\right) \hat{j}$
The magnitude of the displacement vector $r$ is:
$r = \sqrt{((u \cos \theta) t)^2 + ((u \sin \theta) t – \frac{1}{2} g t^2)^2}$
$r = u t \sqrt{1 + \left(\frac{g t}{2u}\right)^2 – \frac{g t \sin \theta}{u}}$
The angle $\phi$ that the displacement vector makes with the horizontal is:
$\phi = \tan^{-1}\left(\frac{y}{x}\right) = \tan^{-1}\left(\frac{u t \sin \theta – \frac{1}{2} g t^2}{u t \cos \theta}\right)$
$\phi = \tan^{-1}\left(\frac{2 u \sin \theta – g t}{2 u \cos \theta}\right)$
Note:
The angle of elevation of the highest point of the projectile ($\phi_{H}$) and the angle of projection ($\theta$) are related by:
$\tan \phi_{H} = \frac{1}{2} \tan \theta$
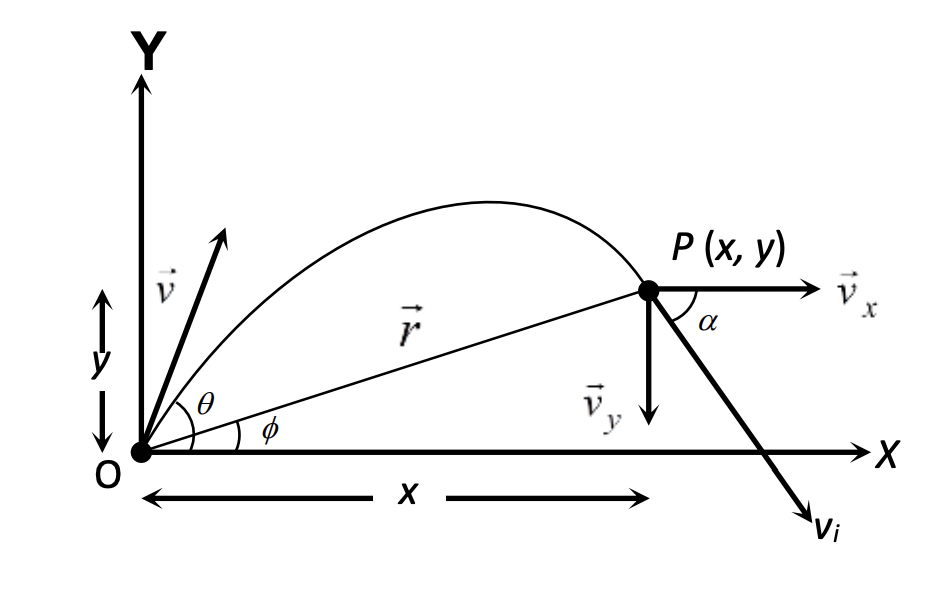
6.5. Instantaneous Velocity ‘$v_i$’
In projectile motion, the vertical component of velocity changes due to gravity, but the horizontal component of velocity remains constant (assuming no air resistance).
Let $v_i$ be the instantaneous velocity of the projectile at time $t$. The direction of this velocity is along the tangent to the trajectory at point P.
Components of instantaneous velocity:
- Horizontal component: $v_x = u \cos \theta$ (constant)
- Vertical component: $v_y = u \sin \theta – g t$
Instantaneous velocity vector:
$\vec{v}_i = v_x \hat{i} + v_y \hat{j} = (u \cos \theta) \hat{i} + (u \sin \theta – g t) \hat{j}$
Magnitude of instantaneous velocity:
$v_i = \sqrt{v_x^2 + v_y^2} = \sqrt{(u \cos \theta)^2 + (u \sin \theta – g t)^2}$
$v_i = \sqrt{u^2 \cos^2 \theta + u^2 \sin^2 \theta + g^2 t^2 – 2 u g t \sin \theta}$
$v_i = \sqrt{u^2 + g^2 t^2 – 2 u g t \sin \theta}$
Direction of instantaneous velocity (angle $\alpha$ with the horizontal):
$\tan \alpha = \frac{v_y}{v_x} = \frac{u \sin \theta – g t}{u \cos \theta}$
$\alpha = \tan^{-1}\left[\tan \theta – \frac{g t}{u \cos \theta}\right] = \tan^{-1}\left[\tan \theta – \frac{g t}{u} \sec \theta\right]$
6.6. Change in Velocity
Initial velocity (at projection point):
$\vec{u}_i = (u \cos \theta) \hat{i} + (u \sin \theta) \hat{j}$
Final velocity (at highest point):
$\vec{u}_f = (u \cos \theta) \hat{i} + 0 \hat{j}$ (since vertical velocity is zero at highest point)
Change in velocity (Between projection point and highest point):
$\Delta \vec{u} = \vec{u}_f – \vec{u}_i = (u \cos \theta \hat{i} + 0 \hat{j}) – ((u \cos \theta) \hat{i} + (u \sin \theta) \hat{j})$
$\Delta \vec{u} = – (u \sin \theta) \hat{j}$
When the body reaches the ground after completing its motion, the final velocity is:
$\vec{u}_f = (u \cos \theta) \hat{i} – (u \sin \theta) \hat{j}$ (since vertical velocity has same magnitude but opposite direction)
Change in velocity (For the complete projectile motion):
$\Delta \vec{u} = \vec{u}_f – \vec{u}_i = ((u \cos \theta) \hat{i} – (u \sin \theta) \hat{j}) – ((u \cos \theta) \hat{i} + (u \sin \theta) \hat{j})$
$\Delta \vec{u} = -2 (u \sin \theta) \hat{j}$
6.7. Change in Momentum
Change in momentum is simply the multiplication of mass ‘$m$’ with the change in velocity.
Change in momentum (Between projection point and highest point):
$\Delta \vec{p} = m \Delta \vec{u} = -m (u \sin \theta) \hat{j}$
Change in momentum (For the complete projectile motion):
$\Delta \vec{p} = m \Delta \vec{u} = -2m (u \sin \theta) \hat{j}$
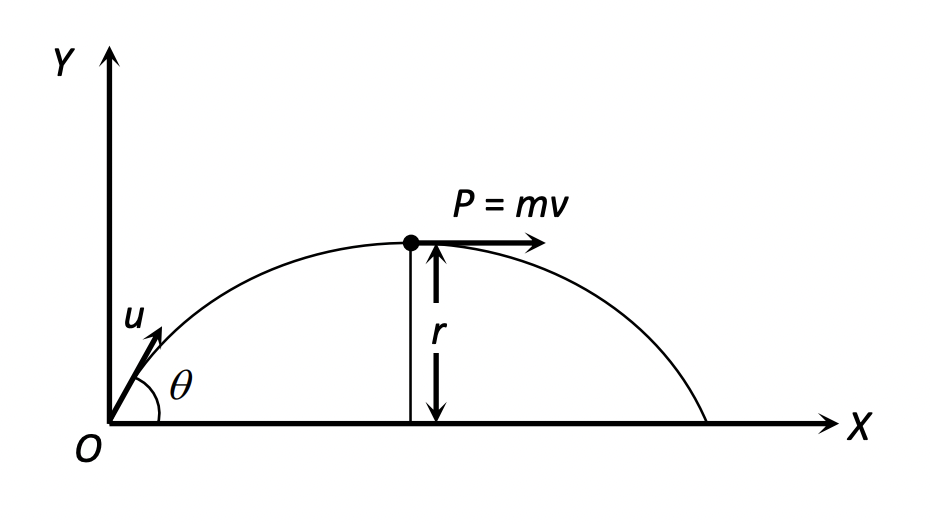
6.8. Angular Momentum
The angular momentum of a projectile at the highest point of its trajectory about the point of projection is given by:
$L = mvr$
At the highest point, the velocity is purely horizontal, $v = u \cos \theta$. The perpendicular distance from the point of projection to the line of action of this velocity is the maximum height $H$.
$H = \frac{u^2 \sin^2 \theta}{2g}$
Therefore, the angular momentum $L$ is:
$L = m (u \cos \theta) \left(\frac{u^2 \sin^2 \theta}{2g}\right)$
$L = \frac{m u^3 \cos \theta \sin^2 \theta}{2g}$
6.9. Time of Flight (T)
The total time taken by the projectile to go up and come down to the same level from which it was projected is called the time of flight.
Consider the vertical motion. At the highest point, the vertical velocity becomes zero. Using the first equation of motion ($v = u + at$) for vertical motion from projection to the highest point ($v_y = 0, u_y = u \sin \theta, a_y = -g$):
$0 = u \sin \theta – g t_{\text{rise}}$
$t_{\text{rise}} = \frac{u \sin \theta}{g}$
Since the time taken to go up is equal to the time taken to come down to the same level (assuming symmetry and no air resistance), the total time of flight $T$ is:
$T = 2 t_{\text{rise}} = \frac{2 u \sin \theta}{g}$
Important Notes on Time of Flight:
- Time of flight can also be expressed as: $T = \frac{2 u_y}{g}$ (where $u_y$ is the vertical component of initial velocity).
-
For complementary angles of projection $\theta$ and $90^{\circ} – \theta$:
- Ratio of time of flight:
$\frac{T_1}{T_2} = \frac{2 u \sin \theta / g}{2 u \sin(90^\circ – \theta) / g} = \frac{\sin \theta}{\cos \theta} = \tan \theta$
$\Rightarrow \frac{T_1}{T_2} = \tan \theta$ - Multiplication of time of flight:
$T_1 T_2 = \left(\frac{2 u \sin \theta}{g}\right) \left(\frac{2 u \cos \theta}{g}\right) = \frac{4 u^2 \sin \theta \cos \theta}{g^2} = \frac{2 u^2 (2 \sin \theta \cos \theta)}{2g^2} = \frac{2 u^2 \sin 2\theta}{2g^2}$
Since $R = \frac{u^2 \sin 2\theta}{g}$, we have $T_1 T_2 = \frac{2R}{g}$
- Ratio of time of flight:
-
If $t_1$ is the time taken by the projectile to rise up to point P (at height $h$) and $t_2$ is the time taken to fall from point P to the ground level, then:
$t_1 + t_2 = T = \frac{2 u \sin \theta}{g}$
The height $h$ of point P is given by:
$\Rightarrow u \sin \theta = \frac{g(t_1 + t_2)}{2}$$h = (u \sin \theta) t_1 – \frac{1}{2} g t_1^2$
Substitute $u \sin \theta = \frac{g(t_1 + t_2)}{2}$:
$h = \frac{g(t_1 + t_2)}{2} t_1 – \frac{1}{2} g t_1^2$
$h = \frac{g t_1^2}{2} + \frac{g t_1 t_2}{2} – \frac{1}{2} g t_1^2$
$h = \frac{g t_1 t_2}{2}$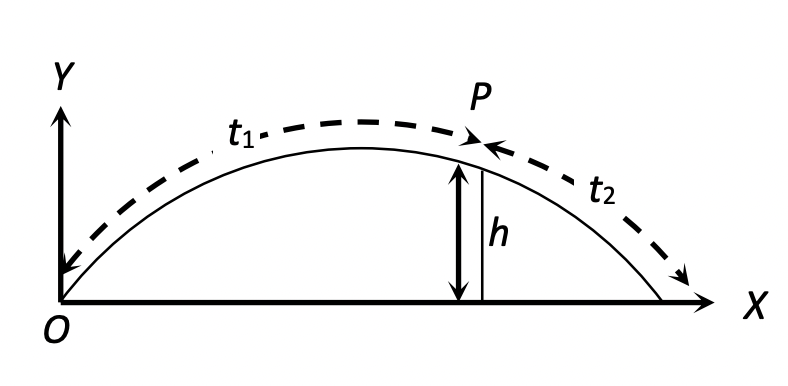
-
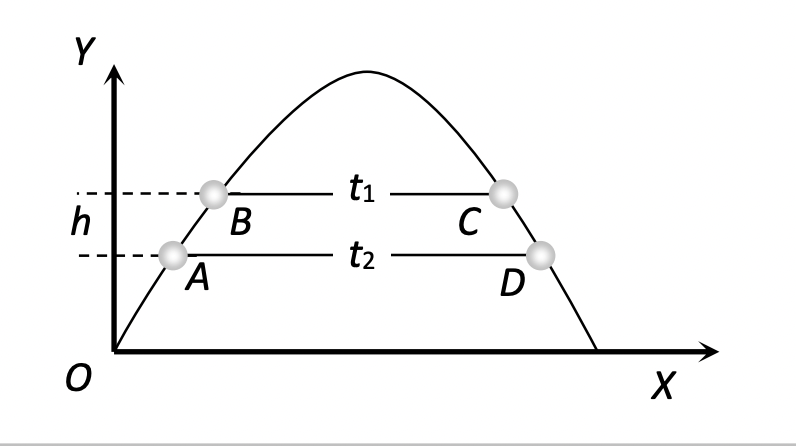
If B and C are at the same level on the trajectory with time difference $t_1$, and A and D are also at the same level with time difference $t_2$, then:
$t_2^2 – t_1^2 = \frac{8h}{g}$
Practice Problem 1 (JEE Advanced Level)
A projectile is fired with a velocity of $50 \, \text{m/s}$ at an angle of $37^\circ$ above the horizontal. (Take $\sin 37^\circ = 0.6$, $\cos 37^\circ = 0.8$, $g = 10 \, \text{m/s}^2$).
Calculate:
- The time of flight.
- The maximum height reached.
- The horizontal range.
Detailed Explanation:
Given: Initial velocity $u = 50 \, \text{m/s}$, angle of projection $\theta = 37^\circ$, $g = 10 \, \text{m/s}^2$.
First, find the components of initial velocity:
$u_x = u \cos \theta = 50 \times \cos 37^\circ = 50 \times 0.8 = 40 \, \text{m/s}$
$u_y = u \sin \theta = 50 \times \sin 37^\circ = 50 \times 0.6 = 30 \, \text{m/s}$
1. Time of Flight (T):
The formula for time of flight is $T = \frac{2 u \sin \theta}{g}$ or $T = \frac{2 u_y}{g}$.
$T = \frac{2 \times 30}{10} = \frac{60}{10} = 6 \, \text{s}$
2. Maximum Height (H):
The formula for maximum height is $H = \frac{u^2 \sin^2 \theta}{2g}$ or $H = \frac{u_y^2}{2g}$.
$H = \frac{(30)^2}{2 \times 10} = \frac{900}{20} = 45 \, \text{m}$
3. Horizontal Range (R):
The formula for horizontal range is $R = \frac{u^2 \sin 2\theta}{g}$ or $R = \frac{2 u_x u_y}{g}$.
Using $R = \frac{2 u_x u_y}{g}$:
$R = \frac{2 \times 40 \times 30}{10} = \frac{2400}{10} = 240 \, \text{m}$
Alternatively, using $R = \frac{u^2 \sin 2\theta}{g}$:
$\sin 2\theta = \sin (2 \times 37^\circ) = \sin 74^\circ$. We know $\sin 2\theta = 2 \sin \theta \cos \theta = 2 \times 0.6 \times 0.8 = 0.96$.
$R = \frac{(50)^2 \times 0.96}{10} = \frac{2500 \times 0.96}{10} = 250 \times 0.96 = 240 \, \text{m}$
Final Answers:
- Time of Flight = $6 \, \text{s}$
- Maximum Height = $45 \, \text{m}$
- Horizontal Range = $240 \, \text{m}$
Practice Problem 2 (JEE Advanced Level)
Two projectiles are fired with the same initial speed $u$, one at an angle $\theta$ and the other at an angle $90^\circ – \theta$ to the horizontal. What is the ratio of their times of flight and their maximum heights?
Detailed Explanation:
Let the first projectile be fired at angle $\theta$ and the second at angle $(90^\circ – \theta)$.
Time of Flight:
For the first projectile ($T_1$):
$T_1 = \frac{2u \sin \theta}{g}$
For the second projectile ($T_2$):
$T_2 = \frac{2u \sin(90^\circ – \theta)}{g} = \frac{2u \cos \theta}{g}$
Ratio of times of flight:
$\frac{T_1}{T_2} = \frac{\frac{2u \sin \theta}{g}}{\frac{2u \cos \theta}{g}} = \frac{\sin \theta}{\cos \theta} = \tan \theta$
Maximum Height:
For the first projectile ($H_1$):
$H_1 = \frac{u^2 \sin^2 \theta}{2g}$
For the second projectile ($H_2$):
$H_2 = \frac{u^2 \sin^2(90^\circ – \theta)}{2g} = \frac{u^2 \cos^2 \theta}{2g}$
Ratio of maximum heights:
$\frac{H_1}{H_2} = \frac{\frac{u^2 \sin^2 \theta}{2g}}{\frac{u^2 \cos^2 \theta}{2g}} = \frac{\sin^2 \theta}{\cos^2 \theta} = \tan^2 \theta$
Final Answers:
- Ratio of times of flight: $\frac{T_1}{T_2} = \tan \theta$
- Ratio of maximum heights: $\frac{H_1}{H_2} = \tan^2 \theta$
6.10. Horizontal Range (R)
It is the horizontal distance traveled by a body during the time of flight.
Using the second equation of motion for horizontal motion ($s = ut + \frac{1}{2}at^2$, where $a_x = 0$):
$R = (u \cos \theta) \times T$
Substitute $T = \frac{2 u \sin \theta}{g}$:
$R = (u \cos \theta) \times \left(\frac{2 u \sin \theta}{g}\right)$
$R = \frac{u^2 (2 \sin \theta \cos \theta)}{g}$
Using the identity $\sin 2\theta = 2 \sin \theta \cos \theta$:
$R = \frac{u^2 \sin 2\theta}{g}$
Important Notes on Horizontal Range:
- Range of projectile can also be expressed as:
$R = \frac{2 u_x u_y}{g}$ (where $u_x$ and $u_y$ are the horizontal and vertical components of initial velocity respectively).
-
If the angle of projection is changed from $\theta$ to $\theta’ = (90^\circ – \theta)$, the range remains unchanged.
$R’ = \frac{u^2 \sin 2\theta’}{g} = \frac{u^2 \sin[2(90^\circ – \theta)]}{g} = \frac{u^2 \sin(180^\circ – 2\theta)}{g}$
This means a projectile has the same range at angles of projection $\theta$ and $(90^\circ – \theta)$, although time of flight, maximum height, and trajectories are different. These angles are called complementary angles of projection.
Since $\sin(180^\circ – X) = \sin X$:
$R’ = \frac{u^2 \sin 2\theta}{g} = R$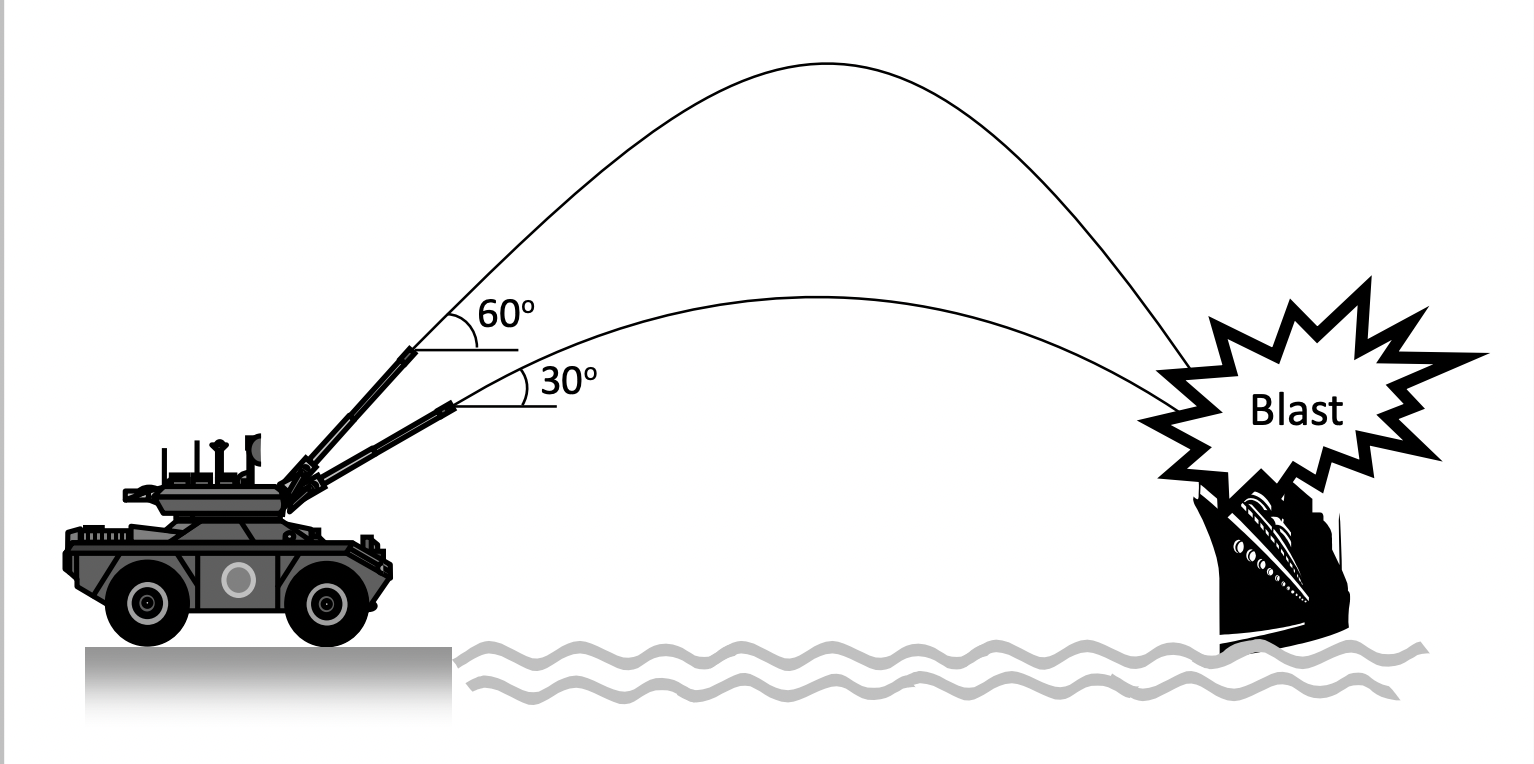
For complementary angles of projection, the ratio of ranges is:
$\frac{R_1}{R_2} = \frac{u^2 \sin 2\theta / g}{u^2 \sin[2(90^\circ – \theta)] / g} = 1 \quad \Rightarrow \quad \frac{R_1}{R_2} = 1$
- For angles of projection $\theta_1 = (45^\circ – \alpha)$ and $\theta_2 = (45^\circ + \alpha)$, the range will be the same and equal to $\frac{u^2 \cos 2\alpha}{g}$. These are also complementary angles.
-
Maximum Range ($R_{max}$):
For the range to be maximum, $\frac{dR}{d\theta} = 0$.
$\frac{d}{d\theta}\left[\frac{u^2 \sin 2\theta}{g}\right] = 0$
$\frac{u^2}{g} (2 \cos 2\theta) = 0$
$\cos 2\theta = 0$
$2\theta = 90^\circ \quad \Rightarrow \quad \theta = 45^\circ$Thus, a projectile will have maximum range when it is projected at an angle of $45^\circ$ to the horizontal. The maximum range will be:
$R_{max} = \frac{u^2 \sin(2 \times 45^\circ)}{g} = \frac{u^2 \sin 90^\circ}{g} = \frac{u^2}{g}$
When the range is maximum ($\theta = 45^\circ$), the maximum height $H$ reached by the projectile is:
$H = \frac{u^2 \sin^2 \theta}{2g} = \frac{u^2 \sin^2 45^\circ}{2g} = \frac{u^2 (1/\sqrt{2})^2}{2g} = \frac{u^2 (1/2)}{2g} = \frac{u^2}{4g}$
Since $R_{max} = \frac{u^2}{g}$, we have $H = \frac{R_{max}}{4}$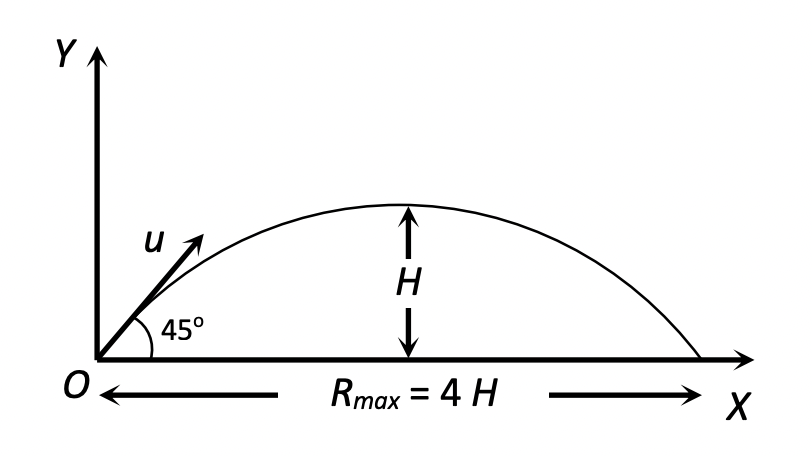
This means if a person can throw a projectile to a maximum distance $R_{max}$, the maximum height to which it will rise is $R_{max}/4$.
Relation between Range (R) and Maximum Height (H):
$R = \frac{u^2 \sin 2\theta}{g}$ and $H = \frac{u^2 \sin^2 \theta}{2g}$
$\frac{R}{H} = \frac{u^2 \sin 2\theta / g}{u^2 \sin^2 \theta / 2g} = \frac{u^2 (2 \sin \theta \cos \theta) / g}{u^2 \sin^2 \theta / 2} = \frac{4 \cos \theta}{\sin \theta} = 4 \cot \theta$
$\Rightarrow R = 4H \cot \theta$If $R = nH$, then $\tan \theta = \frac{4}{n}$ or $\theta = \tan^{-1}\left(\frac{4}{n}\right)$.
- If $R = H$, then $\tan \theta = 4 \quad \Rightarrow \theta = \tan^{-1}(4) \approx 76^\circ$.
- If $R = 4H$, then $\tan \theta = 1 \quad \Rightarrow \theta = 45^\circ$.
Practice Problem 3 (JEE Advanced Level)
A projectile has the same range for two angles of projection. If $T_1$ and $T_2$ are the times of flight for these two trajectories, find the product $T_1 T_2$ in terms of the range $R$ and acceleration due to gravity $g$.
Detailed Explanation:
When a projectile has the same range for two angles of projection, these angles must be complementary. Let the angles be $\theta$ and $(90^\circ – \theta)$.
The time of flight for the first trajectory ($T_1$) is:
$T_1 = \frac{2u \sin \theta}{g}$
The time of flight for the second trajectory ($T_2$) is:
$T_2 = \frac{2u \sin(90^\circ – \theta)}{g} = \frac{2u \cos \theta}{g}$
Now, let’s find the product $T_1 T_2$:
$T_1 T_2 = \left(\frac{2u \sin \theta}{g}\right) \left(\frac{2u \cos \theta}{g}\right)$
$T_1 T_2 = \frac{4u^2 \sin \theta \cos \theta}{g^2}$
We know that the horizontal range $R$ is given by:
$R = \frac{u^2 \sin 2\theta}{g} = \frac{u^2 (2 \sin \theta \cos \theta)}{g}$
From the expression for $T_1 T_2$, we can rearrange it:
$T_1 T_2 = \frac{2 \times (2u^2 \sin \theta \cos \theta)}{g^2} = \frac{2}{g} \left(\frac{u^2 (2 \sin \theta \cos \theta)}{g}\right)$
Substitute $R = \frac{u^2 (2 \sin \theta \cos \theta)}{g}$:
$T_1 T_2 = \frac{2R}{g}$
Final Answer:
$T_1 T_2 = \frac{2R}{g}$